Animations for
|

|
|
This page contains animations for predicted effects arising from relativity violations.
Related links:
Light from relativity violations
Variation of observables with sidereal time
Energy-level shifts in a Penning trap
Does an apple dropped in the summer fall at the same rate as an apple dropped in the winter? The answer may be no.
Many types of relativity violations are possible. They can be understood as an orientation in empty spacetime. For example, one simple set of violations can be visualized as a direction in 3D space and represented by an arrow pointing in the same direction at every point.
A particular class of relativity violations turns out to be detectable only in conjunction with gravity. For example, if all the arrows point the same way when there is no gravity, the violations may be undetectable because all particles feel the same effects. But a gravity-producing body like the Earth curves spacetime in its vicinity and so distorts the distribution of arrows, producing detectable effects. In the presence of these particular violations, an object may fall to the Earth in a changed way but otherwise behave normally.
These particular relativity violations change the gravitational properties of an object according to its motion. One striking effect results from the revolution of the Earth around the Sun. For example, the rate at which objects fall to the Earth can depend on the season. This is illustrated in the animation. The Earth is shown moving around the Sun in a background of red arrows representing the relativity violations. The motion of the Earth and objects like an apple aligns differently with the arrows in the summer and winter, which causes identical apples to fall at different rates in the two seasons. There is also a similar but smaller day-night effect due to the rotation of the Earth.
These violations can also change the gravitational properties of an object depending on its composition. Different objects may therefore fall at different rates, even in the same season. For example, apples could fall differently from oranges. This implies apparent violations of the principle of equivalence, which can be sought in various experiments comparing the behavior of different materials in gravity. It also turns out that particles and antiparticles are affected differently, so the motions of an apple and an anti-apple could also be different. This can be tested in experiments using falling antihydrogen atoms.
The intrinsic size of these particular relativity violations could be comparatively large because the weak gravity force suppresses effects. The distortion is proportional to the gravity field, which is weak, and therefore even a large violation may get distorted only a small amount and have escaped detection to date.
For more information, see:
Matter-Gravity Couplings and Lorentz Violation,
Alan Kostelecky and Jay Tasson,
Phys. Rev. D 83, 016013 (2011).
The archived
preprint is available.
Prospects for Large Relativity Violations in Matter-Gravity Couplings,
Alan Kostelecky and Jay Tasson,
Phys. Rev. Lett. 102, 010402 (2009).
The archived
preprint is available.
Gravity, Lorentz Violation, and the Standard Model,
Alan Kostelecky,
Phys. Rev. D 69, 105009 (2004).
The archived
preprint is available.
Could the existence of light be a consequence of relativity violation? Surprisingly, the answer is yes.
There are two basic kinds of relativity violations: spontaneous and explicit. Spontaneous violation occurs when the equations of the theory are invariant under Lorentz transformations but the solutions are not. Explicit violation occurs when the equations directly violate Lorentz symmetry. Both kinds of relativity violations can be interpreted as involving quantities oriented in four spacetime dimensions everywhere in the vacuum. For explicit violation, these quantities are fixed. However, for spontaneous violation they can oscillate. The oscillations are called Nambu-Goldstone modes.
This animation illustrates these oscillations for a special class of theories, called bumblebee theories, in which the solutions involve a vector in the vacuum. In the animation, red arrows represent the vacuum values of the `bumblebee' vector for the special case when the orientation is in the usual three spatial dimensions. The Nambu-Goldstone oscillations of the vectors are visible.
In many bumblebee theories, the oscillations behave like light waves. In fact, these theories provide an alternative to standard Maxwell electrodynamics. In the quantum version of Maxwell's theory, light consists of massless particles called photons that can travel through empty space. The photons are massless because Maxwell electrodynamics has a special symmetry, called U(1) gauge symmetry, that enforces zero mass. In contrast, in the bumblebee picture, the photons of light are the quantum particles associated with the Nambu-Goldstone oscillations. There is no extra symmetry, but photons are massless because Nambu-Goldstone modes are massless.
So which do you think is more elegant: perfect Lorentz symmetry and perfect U(1) symmetry as in Maxwell theory, or broken Lorentz symmetry and no U(1) symmetry as in the bumblebee theories? At first glance it might seem tempting to think of perfect symmetry as more beautiful. But in practice and in philosophical studies, greater beauty is often associated with slightly imperfect symmetry. Perhaps the same is true in Nature.
In any case, it's ultimately a matter of experiment rather than philosophy. The bumblebee theories predict definite experimental signals that don't occur in Maxwell electrodynamics. Many experiments to search for the associated effects are underway, and many others are planned.
For more information, see:
Spontaneous Lorentz and Diffeomorphism Violation, Massive Modes, and Gravity,
Robert Bluhm, Shu-Hong Fung, and Alan Kostelecky,
Phys. Rev. D 77, 065020 (2008).
The archived
preprint is available.
Spontaneous Lorentz Violation, Nambu-Goldstone Modes, and Gravity,
Robert Bluhm and Alan Kostelecky,
Phys. Rev. D 71, 065008 (2005).
The archived preprint is available.

Experiments in space offer the opportunity of performing very sensitive searches for relativity violations. Among the possibilities are experiments on a satellite comparing the rates of two atomic clocks as their orientation changes. Traditional Earth-based experiments comparing atomic clocks (see the animation Variations of observables with sidereal time) are sensitive only to effects depending on the Earth's rotation axis and 24-hour period, which are fixed. Conducting experiments in space allows much greater flexibility in the rotation axis and periodicity, as well as access to higher speeds in some cases. Future missions on satellites or the International Space Station could compare atomic transitions with enough sensitivity to detect possible minuscule violations of Lorentz and CPT symmetry.
The orbit of a satellite is illustrated in the first animation (click to play). The Earth is seen to move about the Sun along the green ellipse. The satellite is represented by the white square orbiting the Earth. Perturbations cause the satellite orbit to precess, so the motion isn't a simple ellipse relative to the Earth. Note that the periods of the satellite and Earth motions are not to scale.
The white arrow shows the satellite orientation and hence the orientation of the atomic clock. The red arrows represent the quantities (technically, the vacuum expectation values) that produce a directionality for empty space. As the satellite orbits the Earth, the orientation of the atomic clock changes relative to the red arrows and so the clock's rate changes (see the second animation). The straight white lines emerging from the Sun represent the axes of a Sun-based system of celestial-equatorial coordinates (a standard coordinate system for reporting experimental results).
The effect of Lorentz and CPT violation on an atomic clock placed in orbit is illustrated in the second animation (click to play). It shows an atom and some of the atom's energy levels, all part of an atomic clock on a space satellite. The atom is colored in proportion to the frequency of light given by the level separation. As the satellite orbits the Earth, the orientation of the atomic clock changes. This modifies the level spacings of the atom, which produces a different frequency of light and hence a different rate for the atomic clock. Beats can be seen in the cyclic variation of the clock rate. These result from a combination of the orbital frequency of the satellite and a double-frequency component arising from the high speed of the satellite.
For more information, see:
Probing Lorentz and CPT Violation with Space-Based Experiments,
Robert Bluhm, Alan Kostelecky, Charles Lane, and Neil Russell,
Phys. Rev. D 68, 125008 (2003).
The archived
preprint is available.
Clock-Comparison Tests of Lorentz and CPT Symmetry in Space,
Robert Bluhm, Alan Kostelecky, Charles Lane, and Neil Russell,
Phys. Rev. Lett. 88, 090801 (2002).
The archived
preprint is available.
Relativity violations can be interpreted as quantities oriented in four spacetime dimensions everywhere in the vacuum. In this animation, red arrows represent these oriented quantities for the special case when the orientation is in the usual three spatial dimensions.
The presence of these quantities in the vacuum changes the behavior and properties of particles and antiparticles. This is illustrated in the animation in terms of the behavior of a basketball and antibasketball on a balance. Without CPT violation, the basketball and the antibasketball would weigh the same and the balance would be level. In the presence of Lorentz and CPT violation, the two can have different effective weights.
In a laboratory on the Earth's surface, the relative weights of the basketball and antibasketball change as the Earth rotates because the orientation of the balance relative to the red arrows changes. This leads to a cyclic variation in the weight of the basketball and antibasketball over a sidereal day.
Searches for analogous sidereal variations in the properties of various systems have produced impressive bounds on coefficients in the Standard-Model Extension. These have achieved among the best existing sensitivities to relativity violations.
For more information, see:
Lorentz and CPT Tests with Clock-Comparison Experiments,
Alan Kostelecky and Arnaldo Vargas,
Phys. Rev. D 98, 036003 (2018).
The archived
preprint is available.
Constraints on Lorentz Violation from Clock-Comparison Experiments,
Alan Kostelecky and Charles Lane,
Phys. Rev. D 60, 116010 (1999).
The archived
preprint
is available.
Sensitivity of CPT Tests with Neutral Mesons,
Alan Kostelecky,
Phys. Rev. Lett. 80, 1818 (1998).
The archived
preprint
is available.
In conventional electrodynamics, a light ray propagating in empty space consists of electric and magnetic fields oscillating transversely to the direction of motion. The polarization of the light is determined by the direction of the electric field and has two independent polarization components. Both components travel with the same speed, so the light ray propagates without change in its net polarization.
When the rotation symmetry of the vacuum is broken, light still has two polarization components but they travel at a slightly different speed. As a result, the net polarization of a light ray changes as it propagates. This is called birefringence.
Calculations in the photon sector of the Standard-Model Extension show that the polarization change would depend on the frequency of the light in a prescribed way. Two animations are provided here to illustrate these effects.
In the first, the light is shown propagating from a distant galaxy to the Earth (bottom of picture). The instantaneous electric-field vector in a plane transverse to the direction of motion is shown as a black arrow in the 1-2 plane of the electric-field components. This arrow rotates in the plane, with its tip tracing an ellipse.
The polarization of the light is determined by two quantities: the orientation of the ellipse (given by the angle psi), and its shape. The breaking of rotation symmetry causes the polarization and hence the orientation and shape of the ellipse to change as the light travels through space.
The second animation illustrates the frequency dependence of the effect. The polarization ellipse is colored according to the frequency of the light, with a spectrum from red to blue corresponding to frequencies ranging from smaller to larger. The Standard-Model Extension predicts that the orientation and shape of the ellipse vary with the frequency. The animation shows these effects on the ellipse and plots the corresponding change in the polarization angle psi as a function of the frequency.
Sensitive searches for the predicted frequency dependence of the polarization of light received from cosmologically distant galaxies have recently become feasible, thanks to improved techniques for spectropolarimetry of infrared, optical, and ultraviolet light. These searches yield an exceptionally sensitive constraint on rotation violations in empty space.
For more information, see:
Constraints on Relativity Violations from Gamma-Ray Bursts,
Alan Kostelecky and Matthew Mewes,
Phys. Rev. Lett. 110, 201601 (2013).
The archived
preprint is available.
Electrodynamics with Lorentz-Violating Operators of Arbitrary Dimension,
Alan Kostelecky and Matthew Mewes,
Phys. Rev. D 80, 015020 (2009).
The archived
preprint is available.
Astrophysical Tests of Lorentz and CPT Violation with Photons,
Alan Kostelecky and Matthew Mewes,
Astrophys. J. Lett. 689, L1 (2008).
The archived
preprint is available.
Lorentz-Violating Electrodynamics and the Cosmic Microwave Background,
Alan Kostelecky and Matthew Mewes,
Phys. Rev. Lett. 99, 011601 (2007).
The archived
preprint is available.
Sensitive Polarimetric Search for Relativity Violations in Gamma-Ray Bursts,
Alan Kostelecky and Matthew Mewes,
Phys. Rev. Lett. 97, 140401 (2006).
The archived
preprint is available.
Signals for Lorentz Violation in Electrodynamics,
Alan Kostelecky and Matthew Mewes,
Phys. Rev. D 66, 056005 (2002).
The archived
preprint is available.
Cosmological Constraints on Lorentz Violation in Electrodynamics,
Alan Kostelecky and Matthew Mewes,
Phys. Rev. Lett. 87, 251304 (2001).
The archived
preprint is available.
Electrons, muons, and many other fundamental particles have a property called spin, which causes them to behave in some respects like minuscule spinning balls. For a given particle with spin, the orientation of its spin axis can depend on environmental factors. In the presence of a magnetic field, for example, the spin axis rotates about the direction of the field. This is called spin precession.
The CPT theorem implies that in a given magnetic field the rate of spin precession is of the same magnitude (but opposite direction) for a particle and its antiparticle. However, in the presence of CPT and Lorentz violation, the precession rates for a particle and its antiparticle can differ, and this difference can change over the course of a sidereal day.
The animation illustrates this effect for an idealized situation involving a charged particle such as an electron or muon moving in a uniform magnetic field. For simplicity, only the additional spin precession caused by the CPT and Lorentz violation is shown. The particle is shown as a white ball. The magnetic field causes the particle to move in a circle, shown in yellow. The particle moves at uniform speed in the direction shown instantaneously by a striped blue arrow. The axis of the particle's spin is indicated by a striped red arrow. A field of solid red arrows shows the direction of the oriented quantities (vacuum expectation values) arising from the spontaneous Lorentz violation.
The full animation contains six independent sections. The upper two are relevant for the special case of the vacuum quantities oriented vertically upwards. The left-hand one shows a view of the additional spin precession in the laboratory frame caused by the CPT and Lorentz violation. The right-hand one shows a top view from the perspective of the particle.
The direction and magnitude of the effects of the Lorentz violation change cyclically as the Earth rotates (cf. animation 1 above). For an idealized experiment on the Earth's equator these effects disappear a quarter of a sidereal day later, as shown in the middle two sections. After half a sidereal day the Lorentz violation is oriented in the opposite direction, as shown in the bottom two sections. The rate of the additional spin precession caused by CPT and Lorentz violation changes correspondingly.
Experiments with electrons in an electromagnetic trap (see the animation below) and with muons in an accelerator ring can be used to search for effects analogous to these. These experiments have produced some of the sharpest constraints on Lorentz and CPT violation.
For more information, see:
Laboratory Tests of Lorentz and CPT Symmetry with Muons,
Andre Gomes, Alan Kostelecky, and Arnaldo Vargas,
Phys. Rev. D 90, 076009 (2014).
The archived
preprint
is available.
CPT and Lorentz Tests with Muons,
Robert Bluhm, Alan Kostelecky, and Charles Lane,
Phys. Rev. Lett. 84, 1098 (2000).
The archived
preprint
is available.
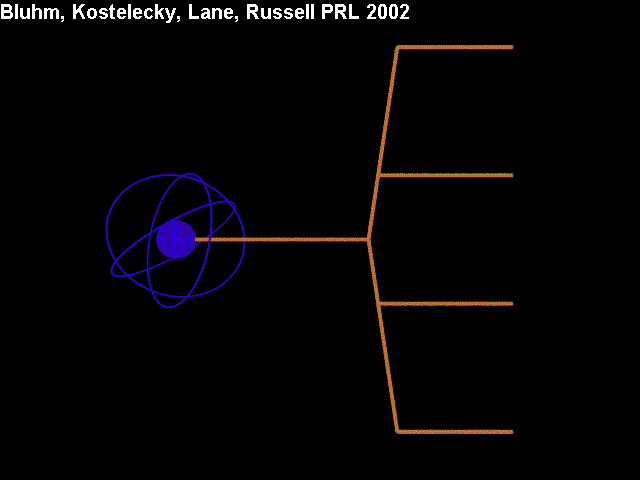
Energy-level shifts in a Penning trap
Electromagnetic traps can be used to confine particles or atoms. For example, a Penning trap confines charged particles using a combination of a uniform magnetic field and a quadrupole electrostatic field. The magnetic field traps each particle laterally by causing it to move along a helix, while the electrostatic field prevents it escaping along the remaining direction.
A single electron in a Penning trap has many quantum energy levels. The dominant structure of the levels is controlled by the magnetic field and consists of a double tower, one for each spin orientation of the electron. It is possible to trap a single charged electron for long periods of time and obtain precision measurements of the spacing between certain levels.
The CPT theorem implies that the double tower of levels for the electron is identical to that of its antiparticle, the positron, except that the spin orientations are reversed. However, in the presence of Lorentz and CPT violation the level spacings can differ and can vary over the course of a sidereal day. These spacings are determined in part by the values of various quantities arising from the spontaneous Lorentz violation, including in particular five coefficients called a0, b3, c00, d30, and c11+c22.
The five animations provided here provide some intuition for the induced level shifts for the distinct types of CPT and Lorentz violation, as produced by different values of these five coefficients. In each animation the two towers of energy levels for the electron are displayed on the left of the image, while the two for the positron are next to them on the right. The values of the five coefficients (zero, positive, or negative) are shown by the positions of the sliders as displayed on the upper right-hand side of the image. The spacing between the levels changes as a given slider is moved back and forth.
In practice, the trapped particles need not be electrons but can also be protons, negative hydrogen ions, etc. Experiments measuring the spacings between certain energy levels for different systems have been performed, producing impressive constraints on Lorentz and CPT violation.
For more information, see:
Lorentz-Violating Spinor Electrodynamics and Penning Traps,
Yunhua Ding and Alan Kostelecky,
Phys. Rev. D 94, 065008 (2016).
The archived
preprint
is available.
CPT and Lorentz Tests in Penning Traps,
Robert Bluhm, Alan Kostelecky, and Neil Russell,
Phys. Rev. D 57, 3932 (1998).
The archived
preprint
is available.
Testing CPT with Anomalous Magnetic Moments,
Robert Bluhm, Alan Kostelecky, and Neil Russell,
Phys. Rev. Lett. 79, 1432 (1997).
The archived
preprint
is available.
You are visitor number
Return to Alan Kostelecky's home or research page